Gougueul Mappe

Présentation

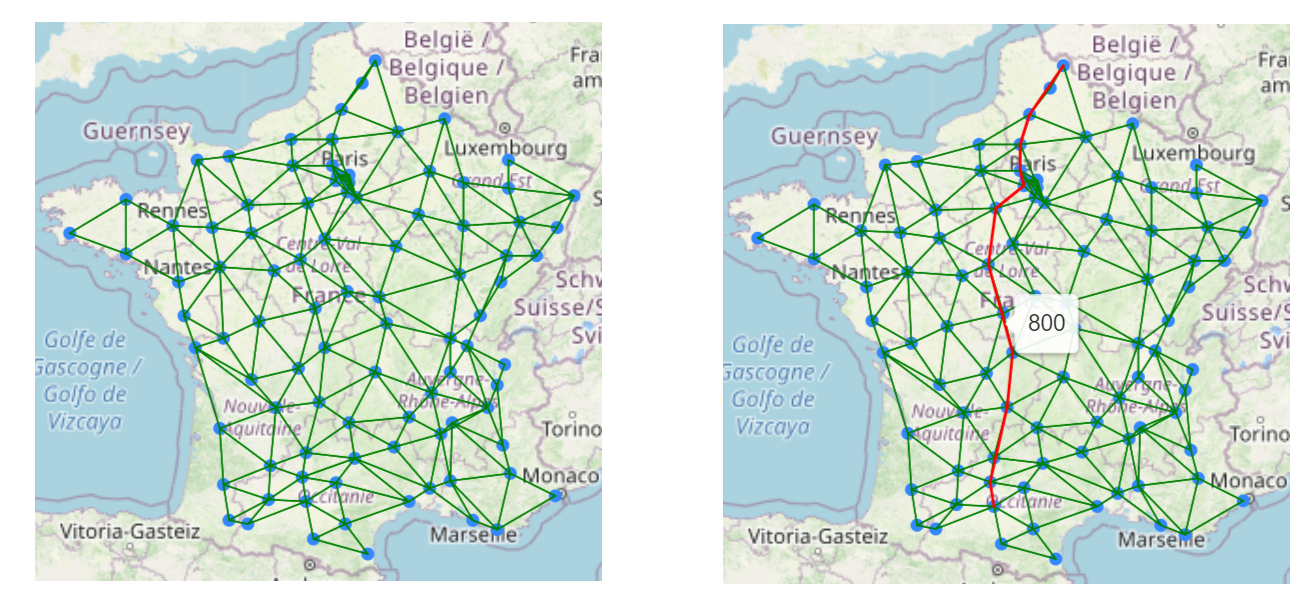
  • Le but de ce projet est de construire un calculateur de plus court chemin routier entre deux destinations. Il s'agit de pouvoir calculer et afficher sur une carte un itinéraire qui relie deux préfectures de France Métropolitaine.

  • Le module python folium servira à afficher la carte, des points pour représenter les préfectures et des segments pour représenter les routes.

  • La structure de données est un graphe dont les sommets sont les villes et les arêtes les routes qui les relient. Ce graphe est pondéré, c'est à dire que pour chaque arête, on prend en compte la distance entre les villes qu'elle relie, en kilomètres. Pour simplifier, on considérera les distances à vol d'oiseau entre les villes et qu'il existe une route uniquement entre deux préfectures de départements limitrophes. La réalité est bien évidemment plus complexe...

  • Les données des préfectures et des liaisons sont fournies dans des fichiers .csv et .txt

  • Le calcul du plus court chemin repose sur l'algorithme de Djikstra (du mathématicien Edsger Wybe Dijkstra, 1930-2002).

Guide de réalisation

On complètera au fur et à mesure le notebook A_Faire.ipynb fourni, découpé en plusieurs zones :

  • Import
  • Classes
  • Fonctions
  • Constantes
  • Carte

La dernière zone "Tests" peut être utilisée pour faire des essais ou débugger une partie du programme.

Etape 1 : La carte

A faire :

  • Installer folium.
  • Afficher la carte de la France métropolitaine.
  • Placer des points de coordonnées gps sur cette carte
  • Tracer des segments qui relie des points.

Etape 2 : Le dictionnaire des préfectures

  • Les données se trouvent dans le fichier prefectures.csv, le séparateur est le point virgule.

  • Les données seront extraites et stockées dans un dictionnaire de dictionnaires python dont voici la structure :

    • Les clés du dictionnaire sont les n° de département (type string).
    • Pour chaque clé, on associe une valeur de type dictionnaire qu contiendra le nom de la préfecture (type string) et les coordonnées gps ( un tuple de deux float).
      • Exemple, voici une ligne de ce dictionnaire : 
        '45': {'ville': 'Orléans', 'gps': (47.90027777777778, 1.910555555555556)}

  • Les coordonnées gps permettent ensuite de placer des points sur la carte.

A faire :

  • Ecrire la fonction data_extract(fichier). Cette fonction prend en paramètre un fichier .csv dont le séparateur est le point-virgule et renvoie un dictionnaire qui contient les informations précédemment décrites( zone "Fonctions" du notebook).

Indication : On pourra se documenter sur la fonction .split() qui permet de manipuler des chaînes de caractères.

  • Extraire les données demandées et les stocker dans la variable PREFS ( zone "Constantes")
  • Afficher toutes les préfectures sur la carte à l'aide de leurs coordonnées gps( zone "Carte").

Etape 3 : Construire et afficher le graphe

  • La fonction distance(A,B) fournie prend en paramètres deux préfectures identifiées par leur n° de département et renvoie la distance qui les sépare, à vol d'oiseau.
    • Exemple : distance('45','41') renvoie la distance Orléans-Blois , 65.44465666820906.
  • La classe Graphe contient des méthodes permettant de représenter un graphe non orienté, à l'aide d'un dictionnaire d'adjacence, mais elle est incomplète.
    • Exemple de ce que doit contenir ce graphe: Les voisines d'Orléans et leurs distances à elle. 
      '45' : {'18': 95.18348914038761, '28': 69.3957162373783, '41': 65.44465666820906, '58': 154.6384323287277, '77': 98.19130122267671, '89': 166.48079450276416, '91': 89.77283144377274}
  • Le fichier voisins.txt contient les départements limitrophes de chacun des départements français. On peut extraire ces données pour construire le graphe.

A faire :

  • Compléter la classe Graphe de telle sorte que la méthode ajouter_arc(self,s1,s2) calcule et stocke la distance s1-s2 dans le dictionnaire d'adjacence( zone "Classes" du notebook").
  • Pour construire le graphe à l'aide du fichier voisins.txt, compléter la fonction construit_graphe(fichier), qui prend en paramètre un fichier texte et qui renvoie un objet graphe avec ses sommets et ses arêtes pondérées( zone "Fonctions" du notebook).
  • Pour afficher le graphe, compléter la fonction affiche_graphe(graphe,carte, prefs). Cette fonction ne renvoie rien, elle utilise le graphe passé en argument, pour modifier la carte passée en argument, à l'aide des données contenues dans le dictionnaire prefs( zone "Carte").
  • Si tout fonctionne correctement, une carte similaire à l'image de présentation en haut à gauche de ce document doit apparaître.

Etape 4 : Afficher des chemins

  • On considère un chemin comme un tableau python contenant les numéros des départements qui constituent ce chemin :
    • Exemple : ['45','41','37','49','44'] est un chemin qui part d'Orléans et qui arrive à Nantes, il passe entre autre, par Tours.
  • On pourra afficher un chemin en traçant une suite de segments, d'une couleur autre que les arêtes du graphe.

A faire

  • Ecrire la fonction affiche_chemin(t,carte,prefs). Elle ne renvoie rien, elle modifie la carte passée en argument pour afficher le chemin t passé en argument à l'aide des données du dictionnaire prefs(zone "Fonctions" du notebook).
  • Tester cette fonction avec quelques chemins définis manuellement( zone "Carte" du notebook).

Etape 5 : Construire et afficher le plus court chemin.

  • L'algorithme de Djikstra permet de déterminer le plus court chemin entre un sommet donné et tous les autres sommets du graphe.Ici on l'arrête dès que l'on a atteint le sommet d'arrivée. Pour comprendre son fonctionnement, on pourra consulter la page wikipédia suivante, en particulier l'animation intitulée "Animation d'un algorithme de Dijkstra" :
  • La fonction dijkstra(graphe,source,fin) prend en paramètres un graphe, le sommet source et le sommet d'arrivée qui sont ici des n° de département. Cette fonction renvoie un dictionnaire dont les clés sont les sommets visités lors de l'éxécution de l'algorithme. A chaque clé est associée un tuple qui contient la distance de ce sommet à la source et le sommet prédécesseur.
    • Ainsi dijkstra( G,'45','94') renvoie le dictionnnaire suivant : 
      {'45': (0, None), '41': (65.44465666820906, '45'), '28': (69.3957162373783, '45'), '91': (89.77283144377274, '45'), '18': (95.18348914038761, '45'), '77': (98.19130122267671, '45'), '94': (105.16588142271829, '91')}
  • On remarque dans l'exemple précédent que 94 est bien dans la liste des sommets visités. On y lit que la distance à 45 est approximativement $105$ km et que l'on accède au sommet 94 à l'aide du sommet 91. On peut ensuite poursuivre le chemin à l'envers : 91 est dans la liste des sommets visités et son prédécesseur est 45. Le plus court chemin de 45 à 94 est 45 , 91 , 94. Reconstruire ce chemin est le rôle de la fonction plus_court_chemin(graphe,depart,arrivee).
  • Il ne reste plus qu'à afficher le plus court chemin choisi par l'utilisateur.

A faire

  • Ecrire la fonction dijkstra(graphe,source,fin). Il est vivement recommandé de bien comprendre le fonctionnement de l'algorithme avant de se lancer dans l'écriture de la fonction( zone "Fonctions" du notebook).
  • Ecrire la fonction plus_court_chemin(graphe,depart,arrivee). Cette fonction prend en paramètres un graphe, le sommet de départ et le sommet d'arrivée, elle renvoie un chemin sous form d'un tableau python.
    • Ainsi plus_court_chemin(G,'45','94) renvoie ['45','91','94']( zone "Fonctions").
  • Afficher des plus court chemins à l'aide de la fonction réalisée à l'étape précédente. Les affichages obtenus seront similaires à l'image de présentation en haut à droite( zone "Carte").

Etape 6 :

  • On pourra bien sûr améliorer ce projet en augmentant le nombre de villes et de liaison, en affichant des informations supplémentaires (distance totale de l'itinéraire, nom des villes traversées,proposer des trajets à étapes, etc...)